The first step of dispersion and dissolution of a powder is wetting; therefore, understdanding the wettability behavior of powders is important in many applications such as inks, paints, food and pharmaceutical industry. The method to characterize powder wettability depends on the powder properties and application purposes. Sessile drop, Wilhelmy plate and liquid penetration (both column and thin film wicking) are common methods for determining the wettability of powders.
Method | Sample | Limits |
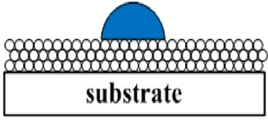
Sessile drop (disc or layer) | Disc: under high pressure (70–700 MPa)
Layer: layer deposited on a substrate from a solution or using an adhesive
|
|
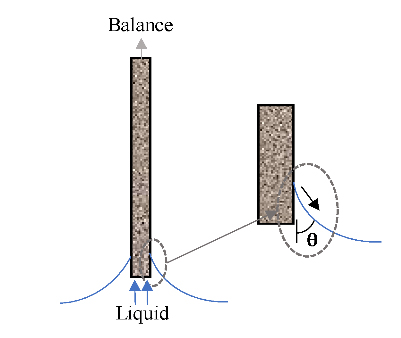
Wilhelmy plate | Powder coated on substrate with or without adhesive or powder compacted into rectangular shapes
|
|
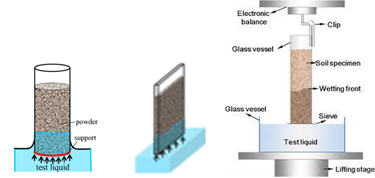
Liquid penetration (column or thin-layer wicking) | Column: powder (~100 mg to < 10 g) packed inside a tube/column with support at the bottom (Washburn capillary rise) Thin-layer: A thin layer of powder deposited onto a substrate from a particle suspension
|
|
Washburn method:
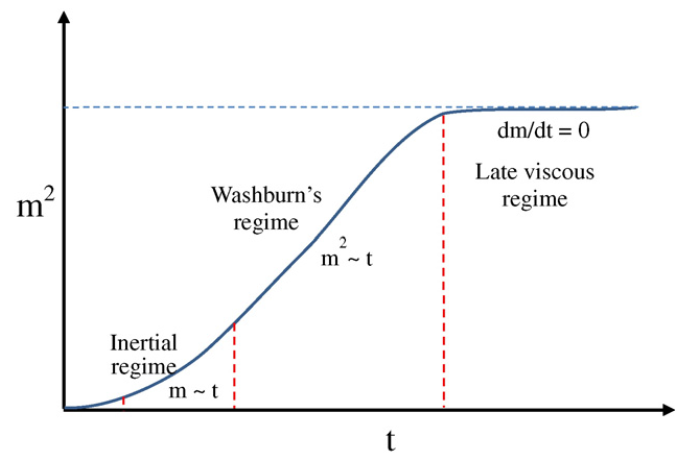
The capillary rise into a packed powder bed generally consists of three basic stages:
The first stage is dominated by the inertial forces; the second stage is governed by the capillary forces (i.e., capillary forces > gravity forces); and the third stage, is dominated by the gravity forces. |
|
Lucas (1918) and Washburn (1921) used momentum balance and by neglecting the effects of gravity and inertial, derived an equation relating the height of penetrating liquid vs. time, Washburn equation:
| (1) |
![\[ {v_{avg}=\frac{r^2ΔP}{8ηh}} \]](https://quicklatex.com/cache3/42/ql_4723aec0d8d5c9823ecd4c09e22a9b42_l3.png "Rendered by QuickLaTeX.com")
where vavg is the average velocity of the liquid, r is the effective radius or the equivalent radius of an individual capillary tube in the capillary bundles, ΔP is the pressure drop, η is the viscosity of the liquid, and h is the height of the liquid flow. Eq. (1) is commonly known as the Hagen–Poiseuille equation. In capillary rise, the pressure drop is:
| (2) |
![\[ {{\Delta}P=\frac{2{\gamma }^{LV}{cos θ\ }}{r}} \]](https://quicklatex.com/cache3/ed/ql_4299edf5af1a61640f16f5252492f7ed_l3.png "Rendered by QuickLaTeX.com")
where γLV is the surface tension of the liquid and θ is the powder contact angle. Using Eqs. 1 and 2 one has:
| (3) |
![\[ {v_{avg}=\frac{dh}{dt}=\frac{r{\gamma }^{LV}{cos θ\ }}{4ηh}} \]](https://quicklatex.com/cache3/58/ql_d617e33ed547b9865b6d42c64ed54a58_l3.png "Rendered by QuickLaTeX.com")
By considering the packed powder as many parallel bundles of capillary tubes and integrating with an initial condition of no rise at time zero, the Washburn equation is obtained:
| (4) |
![\[ {h^2=\frac{r{\gamma }^{LV}{cos θ\ }}{2η}t} \]](https://quicklatex.com/cache3/5a/ql_14de3574035667509fa19e6da64aa75a_l3.png "Rendered by QuickLaTeX.com")
Another way of writing the Washburn equation is based on the lifted mass of liquid:
| (5) |
![\[ {m^2=\left(\frac{A^2{\varepsilon }^2r}{2}\right)\left({\rho }^2\frac{{\gamma }^{LV}{cos θ\ }}{η}\right)t} \]](https://quicklatex.com/cache3/a9/ql_68e5d91ff5bab5b6e3265e15eed064a9_l3.png "Rendered by QuickLaTeX.com")
where A is the cross-section area of the column, ε is the porosity of the packing in the tube, and ρ is the liquid density,. The value of (A2ε2r)/2 should be determined experimentally using a completely wetting liquid (e.g., C6–C10 alkanes). It should be noted that the packing of a powder used to determine (A2ε2r)/2 and that used for the test liquid should be as identical as possible.
Assumptions: continuity, newtonian fluid, incompressible, laminar flow, steady-flow situation, fully developed flow, no-slip, no external pressure and negligible gravitational force.
Jikan CAG Series enable the user to precisely and straightforwardly measure the contact angle of powders through the Washburn method as well as the Sessile drop (disc or layer) method using Jikan Assistant Software.