Polar and Dispersive Components of Liquid Surface Tension - Jikan Surface Nano-Engineering Company

How to calculate the polar and dispersive surface tension components of a liquid?

by JikanGroup

There are two methods for calculating the polar and dispersive surface tension components of a liquid:

pendant drop method (preferred).
sessile drop method.

1. The pendant drop method for measuring the surface tension components of a liquid

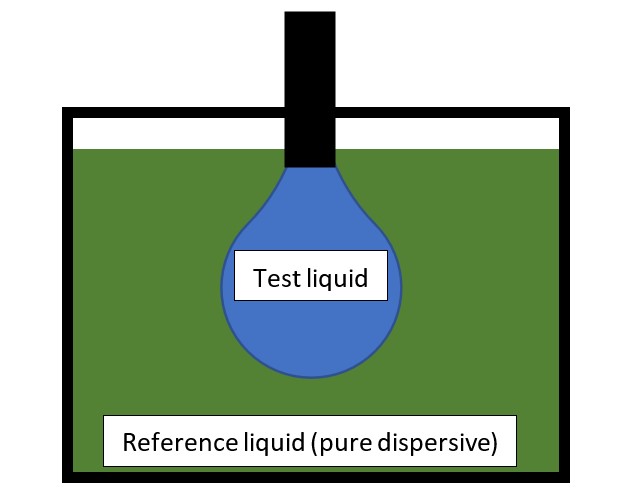
Using the OWRK (Owens-Wendt-Rabel-Kaelble) or geometric mean method, the surface tension between test and reference liquids (also known as the interfacial tension) is calculated as:

${\gamma }_{lr}={\gamma }_l+{\gamma }_r-2\sqrt{{\gamma }^p_l{\gamma }^p_r}-2\sqrt{{\gamma }^d_l{\gamma }^d_r}$

(1)

where γ_lr is the interfacial (surface) tension between test and reference liquids, γ_l and γ_r are the surface tensions of test and reference liquids, accordingly, p and d superscripts show the polar and dispersive surface tension components.

For a strictly dispersive reference liquid, i.e. γ_r=γ_r^d, Eq. 1 becomes:

${\gamma }^d_l=\frac{{\left({\gamma }_l+{\gamma }_r-{\gamma }_{lr}\right)}^2}{4{\gamma }_r}$

(2)

And γ_l^p can be found using Eq. 3.

${\gamma }^p_l={\gamma }_l-{\gamma }^d_l}$

(3)

If using the OWRK method, the value of γ_l^p was found negative, Wu method (harmonic mean) should be used as follows:

${\gamma }_{lr}={\gamma }_l+{\gamma }_r-4\frac{{\gamma }^p_l{\gamma }^p_r}{{\gamma }^p_l+{\gamma }^p_r}-4\frac{{\gamma }^d_l{\gamma }^d_r}{{\gamma }^d_l+{\gamma }^d_r}$

(4)

For a strictly dispersive reference, i.e. γ_r=γ_r^d, Eq. 4 becomes:

${\gamma }^d_l=\frac{{\gamma }_r\left({\gamma }_l+{\gamma }_r-{\gamma }_{lr}\right)}{3{\gamma }_r-{\gamma }_l+{\gamma }_{lr}}$

(5)

And γ_l^p can be found using Eq. 3.

The reference liquid shall be:

immiscible and be able to form a meniscus.
chemically homogenous.
strictly dispersive (and free from polar contaminations)
colourless with a melting point lower than 20°C.

Suggested reference liquids:

Preferably use liquid hydrocarbons (e.g. n-decane, n-dodecane, n-tetradecane and n-hexadecane) but if the test liquid is soluble to hydrocarbon, use perfluorohydrocarbons (e.g. n-perfluorohexane and n-perfluorooctane).

Cleaning of reference liquids:

Hydrocarbon:

distillation
chromatography columns with a minimum length of 60 cm filled with silica gel (e.g. particle size mesh 60). The silica gel with polar surfaces absorbs the polar contaminations (e.g. ketones).

Perfluorohydrocarbon:

does not need cleaning.

After cleaning, for the hydrocarbon and perfluorohydrocarbon, the measurable interfacial tension compared to water shall be at least 52 mN/m and 54 mN/m at 23°C, accordingly.

Storage of reference liquids:

The cleaned n-alkanes shall be stored in light-proof glass bottles in the refrigerator at a maximum temperature of 4°C.

2. The sessile drop method for measuring the surface tension components of liquids

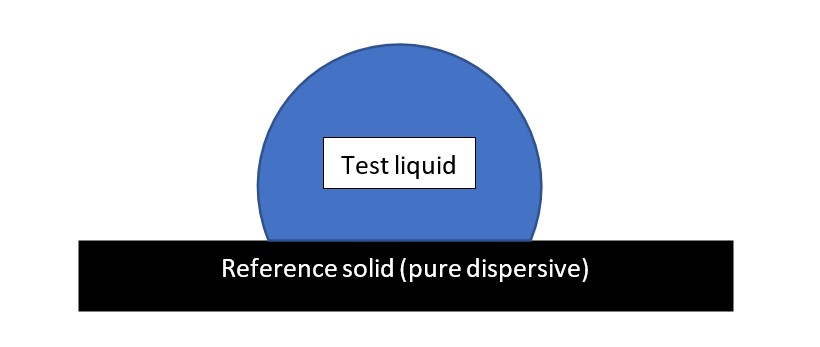
Using the OWRK method (geometric mean), on a pure dispersive solid surface, the relation between contact angle (θ) and surface tension components of the test liquid is:

${\gamma }^d_l=\frac{{\gamma }^2_l{\left(1+{\mathrm{cos} \theta \ }\right)}^2}{4{\gamma }_s}$

(6)

Using the Wu method (harmonic mean), on a pure dispersive solid surface, the relation between contact angle and surface tension components of the test liquid is:

${\gamma }^d_l=\frac{{\gamma }_l{\gamma }_s\left(1+{\mathrm{cos} \theta \ }\right)}{4{\gamma }_s-{\gamma }_l\left(1+{\mathrm{cos} \theta \ }\right)}$

(7)

The polar component of the test liquid surface tension is found using Eq. 3.

Note: For γ_s > 20 mN/m use Eq. 6 otherwise use Eq.7:

The reference solid shall be:

Sufficiently, chemically and topologically homogenous.
Dispersive, e.g. made of paraffin (25.5 ± 0.5 mN/m) or PTFE (18.5 ± 0.5 mN/m).
Where γ_s^p < 0.5 mN/m
Mean roughness value R_a < 0.3 μm

Since Jikan Contact Angle Goniometers (CAG Series) are capable of accurately measuring the contact angle of surfaces via the Sessile Drop method as well as surface and interfacial tensions via the Pendant Drop method, these devices can be utilized to calculate the polar and dispersive surface tension components of a liquid. Jikan Assistant Software can calculate these properties with ease and precision.

Polar and Dispersive Components of Liquid Surface Tension